速读摘要
记得有个妈妈在玩过那期游戏之后,她和孩子在户外运动中,孩子会经常时不时的发现一些螺旋形状的物体,每次孩子发现之后,都会惊喜的喊出来。我们把分形的规律和美感,通过一步步的演示、操作,让孩子了解分形世界的美。如果孩子如果实在没有想法的时候,可以尝试下面规则,让孩子看看遵守这个规则,最后会变成什么图形。我画了一个大的等边三角形,然后在里面继续画三角形,最后得出了下面的图形。这些都是在这个过程中,孩子思维被打开的一个过程。
原文约 2468 字 | 图片 49 张 | 建议阅读 5 分钟 | 评价反馈
给孩子的“分形艺术”|走进自然中的符号世界3
步骤:总结帖:
接上期:
Ki妈说
之前做过2期螺旋的主题游戏,孩子们都非常喜欢。
记得有个妈妈在玩过那期游戏之后,她说,此后,她和孩子在户外运动中,孩子会经常时不时的发现一些螺旋形状的物体,每次孩子发现之后,都会惊喜的喊出来。
我们自然界中,蕴藏着很多美的元素等待着孩子去发现。
这期的分形,比螺旋更普遍。走出去,它几乎存在于自然界中的角角落落。看些看似复杂混沌的事物背后,都是分形在参与其中。

我愿意把分形看成是造物主造物时候用的规则(我用魔咒来给孩子介绍)。
在创造的时候,建立一个简单的规则,就可以把事物从简单变成繁复的万物。就像树木一样,最初,也许造物主的规则,就是让一分为二,于是,就出现了错综复杂的树冠结构。
所以,我们在操作的时候,需要注意引导孩子去自主的设立这样的规则,这有点像,编程代码一样。
分形是从一个整体上取下一部分,这一部分和整体相似,科学家称为自相似性。我们把分形的规律和美感,通过一步步的演示、操作,让孩子了解分形世界的美。
感受分形
准备材料:西蓝花、青菜叶、水芹(香菜叶)、松花皮蛋。
跟孩子聊:
我们生活的大自然中,处处都藏着秘密。
就好像,我现在手中的这颗西蓝花。
把西蓝花掰下一枝,我们好像看到了一朵小小的西蓝花,这朵西蓝花虽然从原来的大西蓝花上掰下来。
但是看上去好像特别像,是一个缩小版的西蓝花。
然后再掰下一朵,又是更迷你的西蓝花。
当我们从一个整体的物体上,取下一小块,这一小块跟整体很相似,我们把这样的图案叫做分形。有的分形会有很多次。就像西蓝花,我们可以看到3次分形。

让孩子找找其他的几种蔬菜上,又没有这种现象。

我特意买了松花皮蛋让孩子观察表面的纹理,这些松花,其实也是分形在参与其中。

进一步感受分形
准备材料:将图片打印或者放在电脑上播放、三个大小有层次的正方形框。
解读:跟孩子一起边看图片,边聊聊。
山的分形结构:

河道的分形结构:

植物的分形结构:
某种海生物的分形结构。
睡莲的分形结构:

龙血树的分形结构,非常的明显,基本每个枝干都遵守一分二的规则




鹿角也有分形结构:

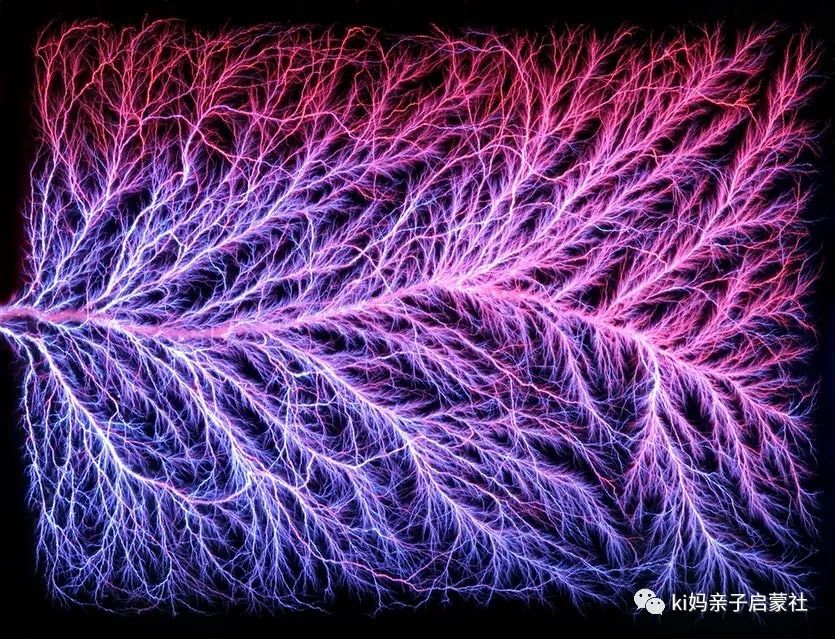
闪电的分形结构:

这期主题之后,在跟孩子户外活动的时候,记得观察身边的大自然,做一下分形结构的探索活动。
造物主的魔咒
准备材料:铅笔、纸、橡皮
步骤:
跟孩子说:
我们会发现,大自然中很多事物都有分形的现象。
就好像造物主的一个魔咒,也许起先他也在为怎么创造这些事物而伤脑筋,后来他念了一个魔咒,于是很多事物就成了现在的样子。
我们来看一下这一条线
(用铅笔在纸上画一条直线)
造物主给出的这个咒语是:让每根线的中间部分,凸出去一个角。
(用橡皮擦把中间的擦掉,画出一个角)
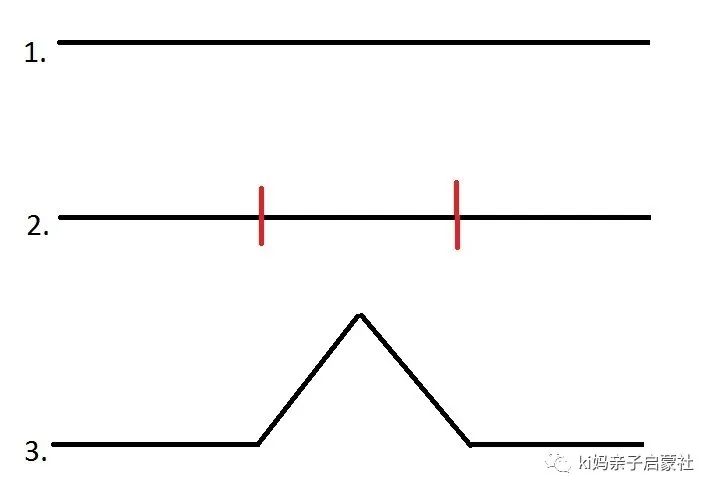
这时候,我们看到又多处来了直线,我们继续在上面画凸出的角
(继续用橡皮擦把中间的擦掉,画出一个角)
如此一直进行下去,直到无法再画为止。
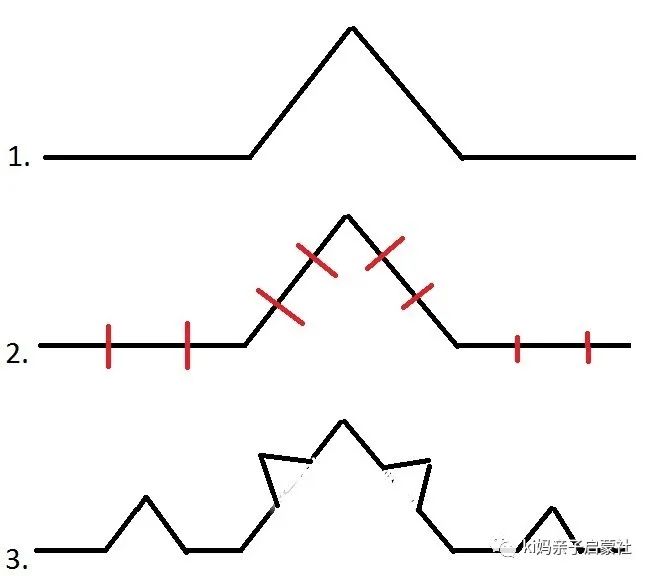
按照规则,同样将所有短的线上,擦掉中间部分,画上凸出的三角。
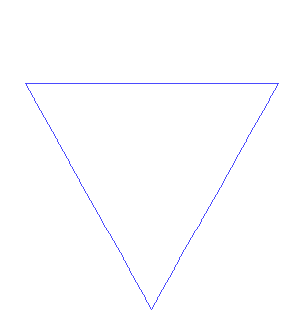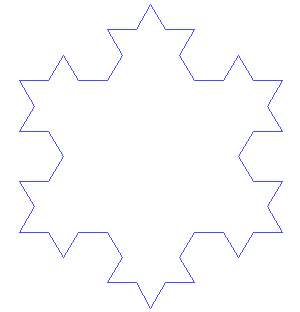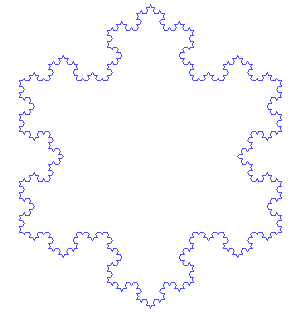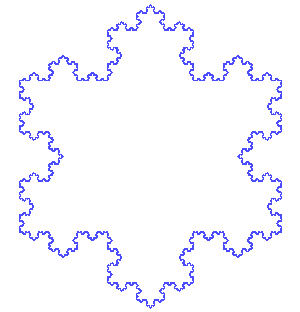
这时候,我们会看到比较复杂但很漂亮的图案。大自然只要一个简单的魔咒,就可以把一根线变成美丽又复杂的图案。

如果这个图形足够大,那么我们可以一直画下去。
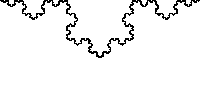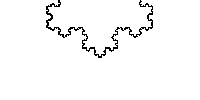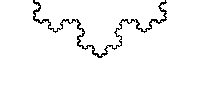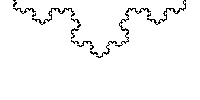
如果有足够的勇气,可以尝试下面的这个图形:
创造分形事物
准备材料:裁剪50个等边三角形。
步骤:
跟孩子说,现在我们再来设置一个魔咒,看看最后会变成什么?
我们用三个三角形,叠成一个大三角形,然后我们重复的叠加这个大三角形:

我们做了4个并排的大三角形。

我们在其中的两个三角形上继续叠加三角形。(中间那部分空开)

我们在其中的两个三角形上继续叠加2个大三角形。

最后,我们在顶部再盖一个三角形。这个图式其实就是非常有名的谢尔宾斯基三角分形结构。

然后让孩子尝试设定其他的规则。我们用6个三角形做了一个正六边形,然后重复正六边形。


在过程中,我们得到了一个空白的正六边形图案,Kiki非常兴奋。

期待你们做更多的尝试。
自主创建规则进行设计
如果孩子如果实在没有想法的时候,可以尝试下面规则,让孩子看看遵守这个规则,最后会变成什么图形。
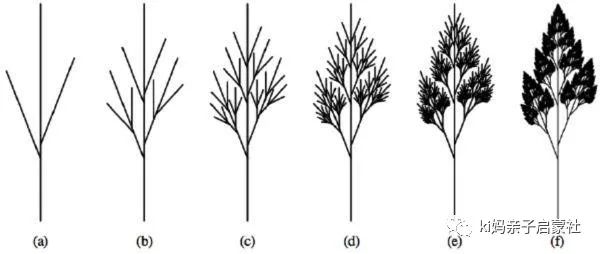
规则1:“在直线的一端分2叉。”
Kiki设置为两段都分叉,画出了这个模型,她说看起来就像叶脉的结构。
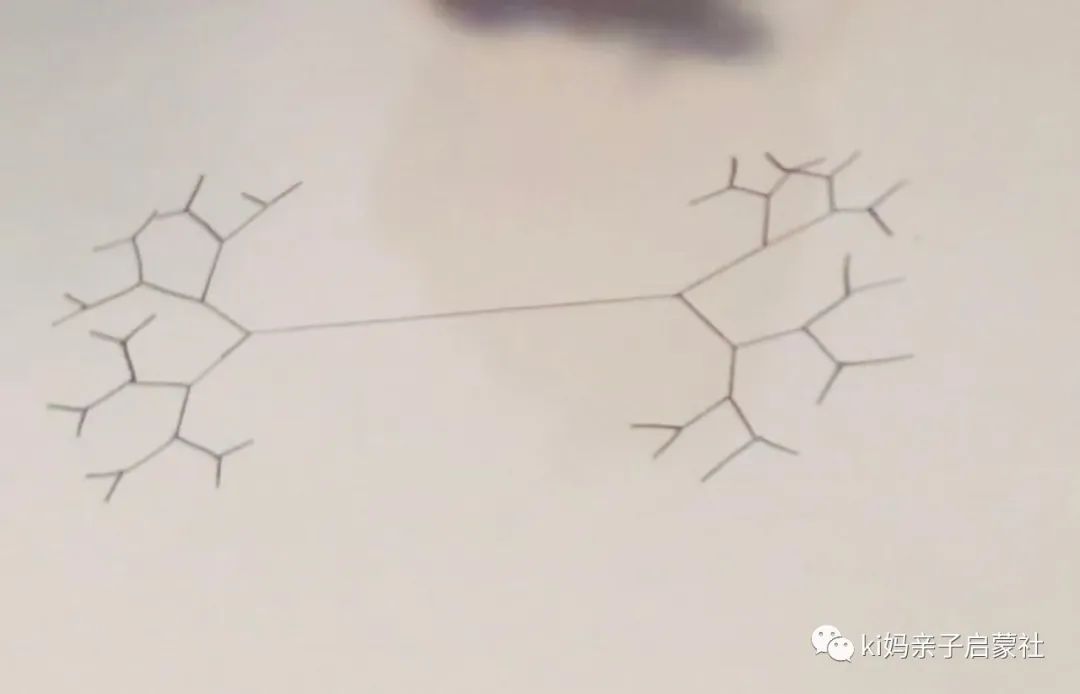
我用偏曲线的方式来创作了树形结构。

也可以尝试一下一分三的结构,很灵活。
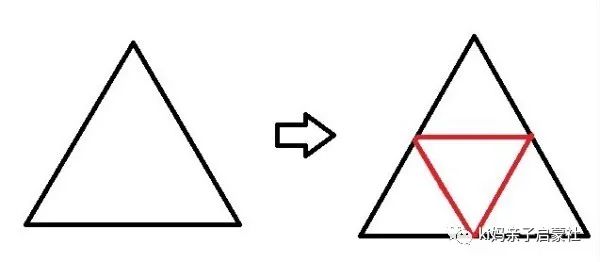
规则2:“在等边三角形内部增加一个同样的三角形。”
我画了一个大的等边三角形,然后在里面继续画三角形,最后得出了下面的图形。
最后的作品是这样的:
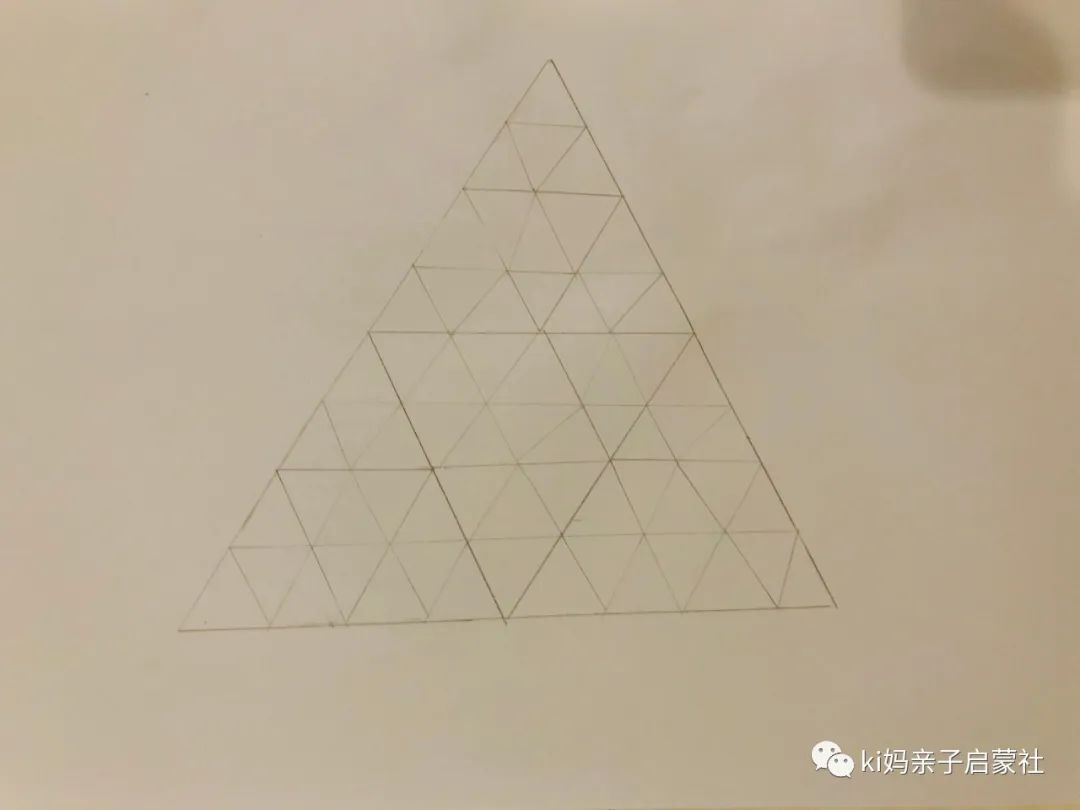
但是kiki在里面重复的画更小的等边三角形。
画的过程中,她有了新的想法,她在最里面的三角形里画上了一个在躺椅上晒太阳的小女孩,旁边还有一条小狗。


最后的成图是这个:

规则3:
可以挑战一下毕达哥拉斯树,如下图,重复一个比较复杂的图案,最后得出一颗毕达哥拉斯树。
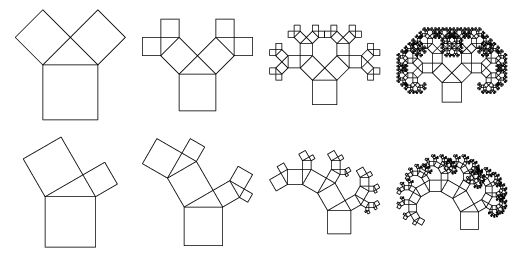
自由创作
自由创作的要求,是提示孩子,可以用到一些分形结构,但是不局限于固定使用具体某一种,Kiki用了螺旋的分形结构来创作了一匹小马。
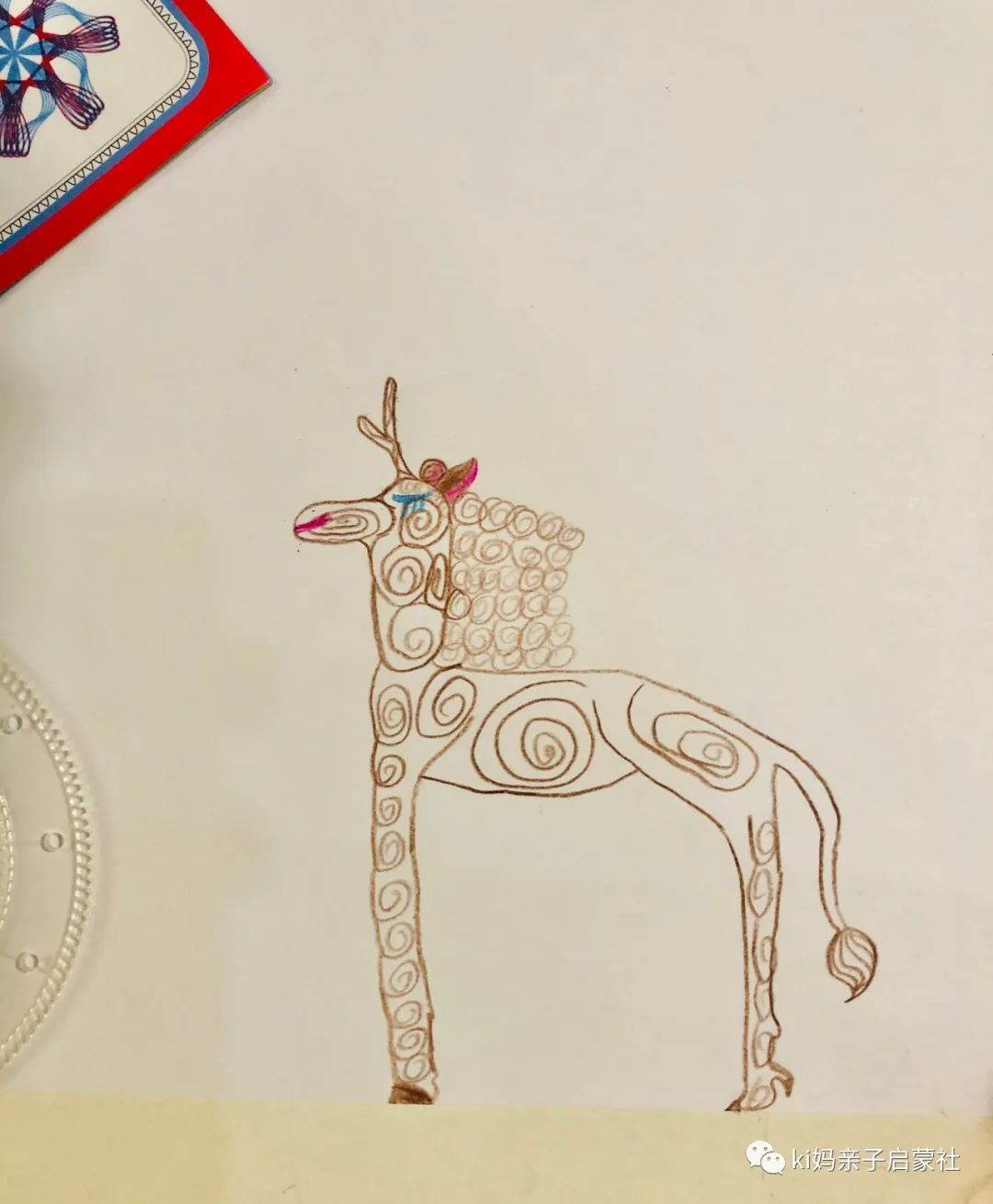
最后,这匹小马给了她新的想法,她又创作了另外一幅神兽图:马头龙角,鹰脚狮尾的神兽。
这些都是在这个过程中,孩子思维被打开的一个过程。


分形设计展
这些是分形设计在很多现实场景中都有应用,跟孩子一起来找找看:





如何获取本期配套素材?
免费下载方式如下:
关注本公众号“ki妈亲子启蒙社”,在首页对话框回复“分形”,即可获取。
资源有效期为7天!
Ps:如果资源已经过期,请前往“Ki妈蒙氏”小程序,自助下载。

蒙特梭利数学的优势是引导孩子从感官数学进入到抽象数学,建立对数学的基础认知。
由蒙特梭利AMI6-12岁阶段的主教Ki妈带领,分享3-12岁,如何对孩子的数学进行启蒙和引导,感兴趣的,请申请进入蒙氏数学学习营。

扫二维码,暗号“数学”,申请进入数学学习营,群满为止,已入ki妈群的不用重复加入。



在看
