09、加法初接触｜加法

 

今天这期是数学启蒙，真正开始引导孩子学习运算。其实之前或多或少跟kiki提起过，kiki外婆也经常在睡前跟她玩加法游戏。今天的这个主题游戏是让孩子接触加法，并学会用数学符号去表示加法。

 

分享一个游戏里面的感触，教具作为早期孩子接触数学的工具，非常重要。

 

这个主题游戏其实玩的时间非常长，本身数学在我们看来是有点枯燥的，但是通过教具和游戏相结合，孩子动手操作起来，就觉得是在完成一项探索任务，时间在不知不觉中飞逝。

 

 

而教具操作的意义，就在于给了孩子图式的经验。人类思维的发展就是从经历和体验中抽象出定律和规律，形成与现实相吻合的图式。最后一步就是图式化，它和公理化、形式化相对应，图式化就是形式内容的内化过程，其结果是一种心理意义，即心理结构。

 

我们说的数感，应该就是这种经验规律的内化为心理图式，可以让孩子想都没想，就快速的凭感觉做出判断。后面游戏中，我会提到具体的实践感触。

 

 

 

有一段时间没有接触数棒了，拿出来排列的时候，kiki觉得很新鲜，飞快的排起来。进行了两个奇偶数的主题，今天来回顾一下。

 

这个简单的游戏让我感触很深。

 

我们之前的几期，都是按照有没有落单的来判断奇偶。只在百数表里面，简单的观察到了奇偶的规律。

 

这次，当我让kiki快速将奇数的数棒往下移动一格，他只需要判断第一个奇数，之后，就直接按规律排列。（以前，他都是需要反复确定具体数量，一个一个去判断的）说明，奇偶规律已经通过他的经验内化为图式。他已经可以灵活运用在抽象数字和实物上面，我们说的数感，大体应该就是这个意思吧。

 

 

按奇偶规律排列好的数棒，又再次加强了孩子对奇偶的理解。后面，我又让他把全部是偶数的向下拉一格，说出这个数量：2、4、6、8，并让他记住这串数，后面会用到。

 

 

迷你数棒是我们这个蒙氏系列里面涉及的第二套购买的成本教具，之前的教具，我能自己制作就自制。因为能玩很久，所以，我买了下来。

 

迷你数棒，和加法表集合，帮助孩子直观感知数量的加法。

 

这个游戏就是先来熟悉迷你数棒，其实是红蓝数棒的缩小版，也少了分隔，比大数棒更抽象一点。kiki还是很快速的排列好。

 

 

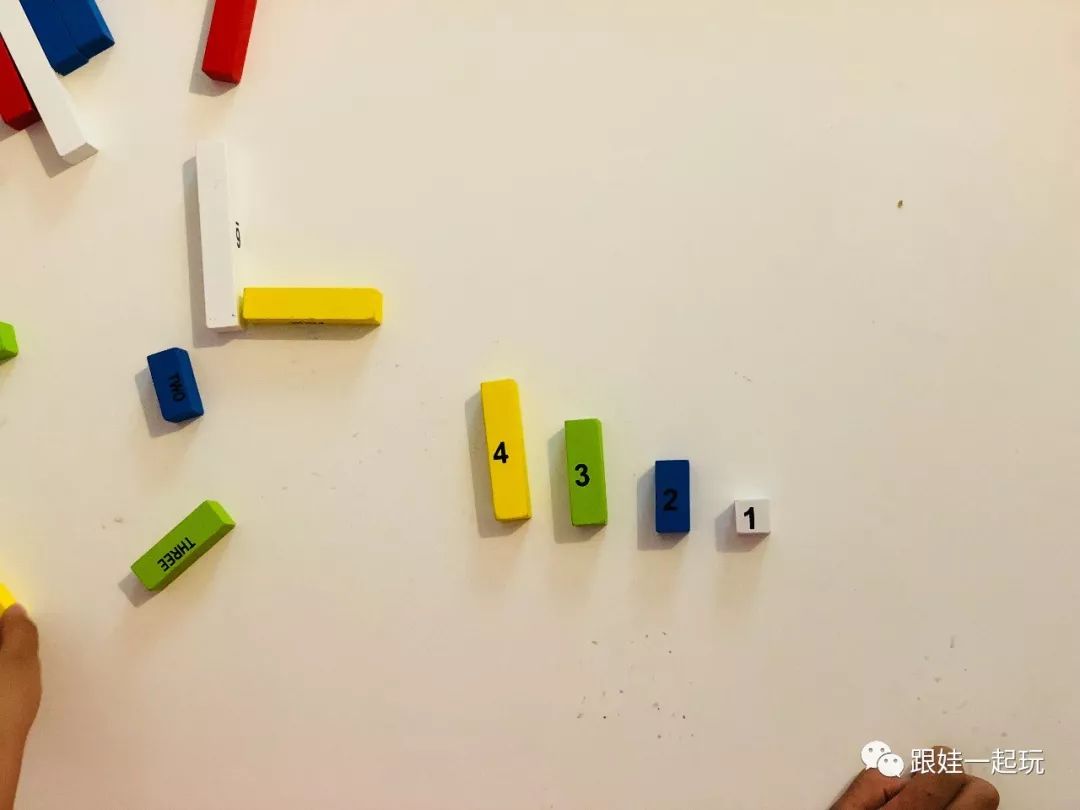
让kiki找“外国数棒”朋友帮忙，凑10，除了让她了解数和数之间的关系之外，也能够通过直观的数棒排列形式，感受到那种互补。

 

 

下图就很明显的能够看到两组数棒阶梯状互补，每段数量都是一样的10。

 

 

 

我特意设计了和数棒颗粒大小匹配的加法表，来帮助孩子进行具象的加法。

 

这样当孩子数棒相加的时候，她可以直接通过数棒长度对应的格子数量来数出总数。这样操作的方式，有点像作实验记录。

 

 

通过相同长度的数棒相加，希望kiki能够对偶数有更深的感觉，相同数量数棒依次相加，得出的是2、4、6、8、10、12、14、16、18，其中，2、4、6、8就是游戏1中，让她记住的偶数串。

 

 

数量大的，同样通过数格子来做，这时候，手指头都不够数了。

 

 

等到相同数相加之后，我们可以观察到数量的增长图式。同时我用双手手指两两相对，慢慢的逐渐演示手指从2、4、6、8、10这样增加的过程，让孩子感受到2、4、6、8、10这串偶数组，是怎么再次出现的。

 

接下来，利用加法表，我们重新又算了怎么将两个数字凑成10，再次，去关注凑成10的数量对应关系，同时，在图表中展示出来。

 

 

 

这套表后续可以经常在做加法的时候拿出来使用，联系。同时不定期的鼓励孩子将加法表填充完整。

 

这次就不用一次全部补充，因为工作量很大，对孩子的脑力是很大的考验。

 

 

数学是将具体事物抽象化，所以，对于等式以及大小符号，有必要跟孩子去谈及。所以，这里面又单独作为一个游戏来给孩子演示。

 

特别是 “<” 、”>”的符号，更为形象。孩子一看就能懂，我告知了大于符号，他也可以推出小于符号。

 

后面会专门抽一主题出来，跟孩子讲讲，人们是怎么样将具体事物进行抽象化的，不仅仅是数字。

 

 

 

最后引出等于符号，后面我们就开始接触加法等式。

 

 

 

 

打印素材，我给了一张等式格式表，这样大家可以经常打印出来，然后自己填写数字来出题，或者孩子可以出题，来让父母做题。

 

我跟kiki是轮流做题，下面的数量是kiki说出数字，我来写进的，然后跟kiki来轮流完成，这样孩子比较容易接受，好像就是游戏一样。

 

 

为什么加法要这么麻烦的向孩子引导？而不是直接算加法？为什么我不赞成只是刷题？

 

其实这里面有中数学思维的引导在里面。我们常听到建模，建模是数学化的一格方面，模型是不可缺少的一个中介。建模就是用模型把复杂的现实和理论来理想化或者简单化，从而更易于进行形式的数学处理。

 

数学化分为两种：一种是水平数学化，这种数学化的过程就是从背景中识别数学，然后图式化——形式化——寻找关系和规律——识别本质——对应到已知的数学模型（现实的、经验的）。

 

水平数学化的过程就是从“生活世界”到“符号世界”的转化过程。

 

这也是我为什么需要引导孩子去关注具象事物和数学符号怎么样通过各种方式结合、配合、并且相互转化的，后面会着重去加强孩子这种符号语言的转化能力，从这方面去培养她的数学思维。

 

当然，另一种数学化是垂直化，就是比较高级的。从低层数学到高层数学的数学化。主要是指符号世界里，符号的生成、重塑和被使用的高级过程。这个目前孩子暂时还不会涉及到。